Praštevila

Definicija

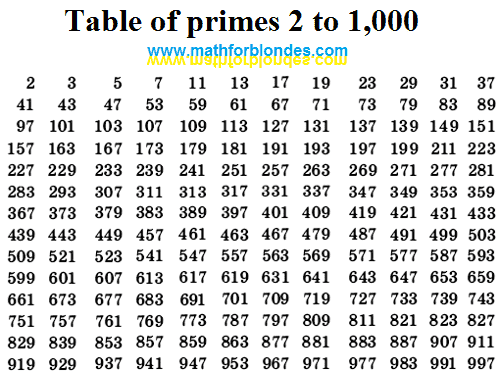
Praštevila so naravna števila, večja od 1, ki imajo natanko dva delitelja: 1 in samo sebe. To pomeni, da jih ni mogoče zapisati kot produkt dveh manjših naravnih števil. Med prva praštevila štejemo 2, 3, 5, 7, 11 in 13. Število 2 je edino sodo praštevilo, saj je vsako drugo sodo število deljivo z 2 in zato ni praštevilo.

Izreki

Eden izmed najstarejših in najpomembnejših rezultatov o praštevilih je Evklidov izrek, ki pravi, da praštevil ni končno mnogo. Evklid je to dokazal z elegantnim argumentom protislovja: če bi bilo praštevil končno, bi lahko ustvarili novo praštevilo tako, da bi vse obstoječe pomnožili med seboj in prišteli 1. Drug pomemben rezultat je Izrek o razcepu na praštevila, ki pravi, da se vsako naravno število večje od 1 da enolično zapisati kot produkt praštevil.

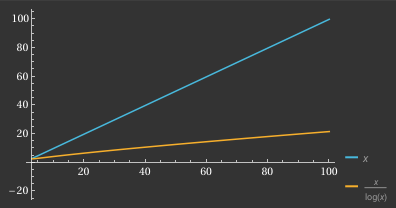
Porazdelitev praštevil med naravnimi števili je dolgo časa burila matematike. Izrek o praštevilih pravi, da je približno toliko praštevil, kolikor je števil manjših od danega števila n, kot je n / ln n. To pomeni, da praštevila postajajo redkejša, ko števila rastejo, vendar jih nikoli ne zmanjka. Kljub temu še danes ne poznamo natančnega vzorca, po katerem se praštevila pojavljajo.

S praštevili je tesno povezan tudi Fermatov mali izrek, ki pravi, da za vsako praštevilo p in vsako celo število a, ki ni deljivo s p, velja a^(p−1) ≡ 1 (mod p). Izrek je temelj modularne aritmetike in se pogosto uporablja pri preverjanju praštevilskosti ter v kriptografskih algoritmih, kot je RSA. Gre za eno najlepših povezav med teorijo praštevil in praktično uporabo v računalništvu.

Ko pa smo že omenili računalništvo, si lahko ogledate še nekaj najbolj osnovnih algoritmov za praštevila.